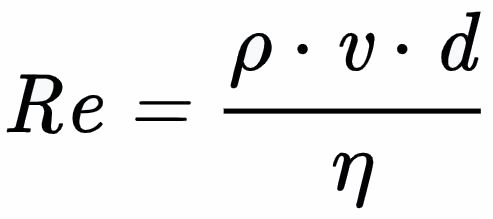Was sagt uns die Reynoldszahl?
Ergänzung am 21. Mai 2023 von Horst Fries:
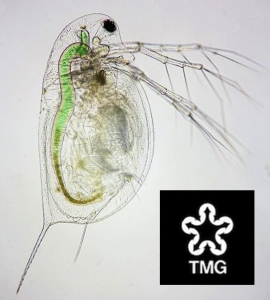
Wie „fühlt“ ein Kleinstlebewesen sein umgebendes Fluid? (Leben bei kleiner Reynoldszahl)
Wo kommt die Reynoldszahl her? Was sagt sie aus und was sagt sie nicht aus? Warum wird sie oft falsch interpretiert?
Ein Vortrag von Horst Fries beim Tübinger Mikroskopischen Stammtisch am 2. Januar 2022.
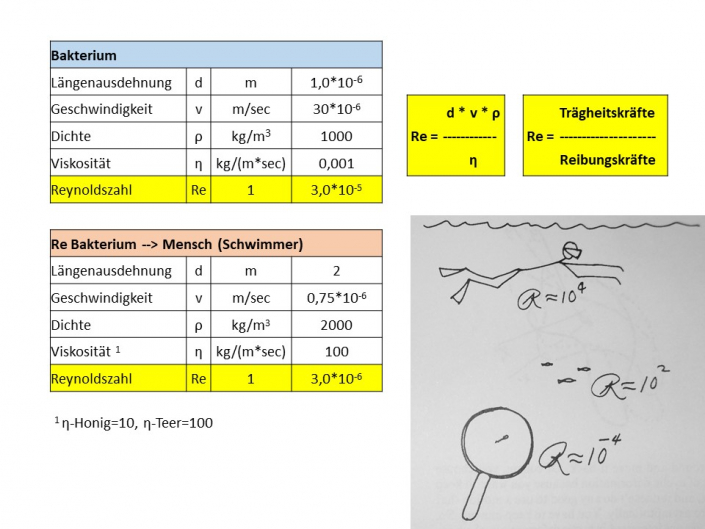
Die Reynoldszahl scheint oft fehlinterpretiert zu werden. Im Vortrag wird versucht darzustellen, wie die Reynoldszahl aufzufassen ist und was es für das Leben im Mikrobereich bedeutet. Die Auffassung, dass für Kleinstlebewesen sich das Wasser zähflüssig (wie z. B. Honig) verhält, kann so pauschal nicht richtig sein. Denn das kann nicht die sehr flinken Bewegungen von Kleinlebewesen oder das schnelle Schlagen von Cilien erklären.
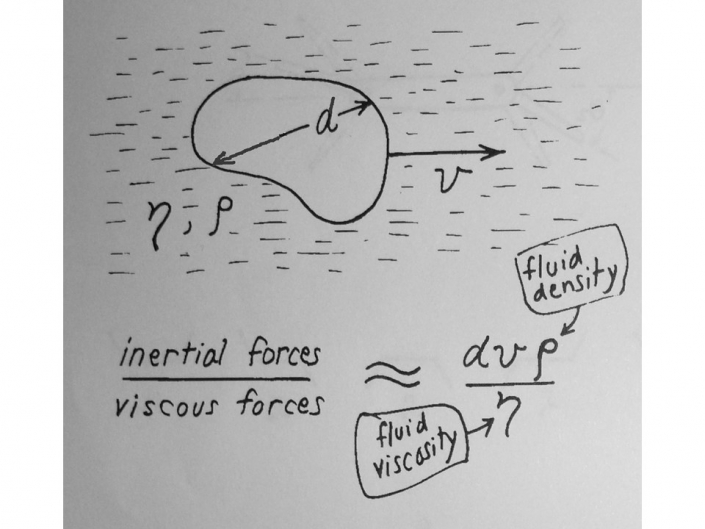
Die Reynoldszahl sagt aus, dass im vergrößerten Maßstab die Strömungsverhältnisse durch ein zäheres Fluid nachgebildet werden können. Vielmehr ist entscheidend, dass in sehr kleinen Dimensionen das Verhältnis von Trägheitskräften und Reibungskräften (was ebenfalls der Reynoldszahl entspricht) sehr klein ist, so dass die Trägheit (des Fluids!) vernachlässigt werden kann. Kleine Trägheit des Fluids bedeutet kein Nachfließen, also augenblicklicher Stopp der Strömung, wenn keine Kraft mehr auf das Fluid wirkt. Ebenso wirkt keine nennenswerte Trägheit des Fluids auf das Kleinlebewesen ein, so dass es mit minimalem Kraftaufwand im Fluid beschleunigen kann.
Die Reibungskraft ist indes nicht zu vernachlässigen, im Gegenteil: Nach Stokes ergibt sich für die Reibung eines kugelförmigen Körpers in einer Strömung
FR = 6 * pi * η * r * v
Das bedeutet, dass die Reibungskraft proportional mit dem Radius r (nicht quadratisch, wie man vermuten könnte!) und der Geschwindigkeit v einhergeht.
D. h. bei Verkleinerung um Faktor n ergibt sich eine Verkleinerung der Trägheitskraft um n3 und eine Verkleinerung der Reibungskraft um n2 (wenn man voraussetzt, dass auch die Geschwindigkeit um Faktor n zurückgeht).
Daraus folgt, dass mit einer Verkleinerung der Größe die Trägheitskraft sich n-mal mehr verringert als die Reibungskraft, die Reibung also die dominierende Kraft wird. Das sagt ja auch die Reynoldszahl als Verhältnis der Trägheitskraft zur Reibungskraft aus.
Kleine Lebewesen müssen also praktisch nur die Reibung überwinden, um eine Geschwindigkeit aufrecht zu erhalten. Für die Überwindung der Trägheit des Fluids zu seiner Beschleunigung ist nahezu keine Kraft erforderlich (bei Re << 1). Daher kommen sehr kleine Lebewesen ruckartig von 0 auf eine Maximalgeschwindigkeit. Die Maximalgeschwindigkeit wird durch die Reibungskraft begrenzt, außerdem natürlich auch durch deren Antriebsmechanismen. Man kann nun schon sagen, dass je kleiner Kleinlebewesen sind, das Fluid im Verhältnis zu ihrer Größe einen größeren Reibungswiderstand hat. Die Viskosität η des Fluids ist deswegen aber nicht größer. Andererseits könnten (ich weiß es aber nicht) Lebewesen, je kleiner sie sind, überproportional zu ihrer Größe eine größere Antriebskraft haben (vergleiche die Tragkraft der Ameise im Verhältnis zu ihrer Größe), so dass die erhöhte Reibungskraft daher für sie leicht überwunden werden kann. Das würde erklären, warum so kleine Lebewesen wie Bakterien hurtig durch die Gegend schwimmen, wie Heribert Cypionka eindrucksvoll mit dem „schnellsten Bakterium der Welt“ demonstriert hatte!
Bei fliegenden Lebewesen kommt natürlich das Gewicht zusätzlich ins Spiel. Der Fransenflügler hat m. E. deshalb fransige Flügel, damit er wegen seinem kleinen Gewicht (das mit der 3. Potenz von der Länge abhängt) nicht durch zu viel Auftriebskraft durch die Flügel (Flügelfläche geht mit der 2. Potenz) unnötig „herumzappeln“ würde und somit durch seinen Fransenflügel einen gleichmäßigeren Flug erreicht. Beim Fliegen hängen aber so viele Faktoren zusammen, dass dies nur eine Spekulation meinerseits ist. Rauhigkeiten und Borsten an Flügeln bewirken bei Insekten (auch bei Vögeln) Turbulenzen an der Flügeloberseite, die wegen Bernouillis Gesetz (erhöhte Strömungsgeschwindigkeit bewirkt Unterdruck) einen zusätzlichen Auftrieb verursachen.
Es zeigt sich auch, dass der Wirkungsgrad für den Antrieb von sehr kleinen Lebewesen wie Bakterien sehr gering (ca. 1%) ist. Das spielt aber offenbar keine Rolle, da extrem wenig Energie gebraucht wir, um sich im Fluid zu bewegen. Weitere Folgerungen sind den Vortragsfolien zu entnehmen.
Die Handskizzen sind dem berühmten Vortrag von E. M. Purcell von 1976 entnommen: „Life at low Reynolds number“, in dem auch interessante Folgerungen erläutert werden. Das PDF des Vortrags gibt es hier → Life at low Reynolds number
Sehr viele Artikel zur Reynoldszahl lavieren sich um diese sehr interessante Problematik herum und erklären die Zusammenhänge unbefriedigend.
Fragen zum Thema und Kritiken zu den obigen Ausführungen wollen wir gerne in kommenden Stammtischen behandeln.
Weitere Artikel im Internet zum Thema:
→ B. Rodewald und H.-J. Schlichting: Wenn Wasser schlüpfrig und Luft klebrig wird (Der vorletzte Satz des an sich gut verständlichen Artikels ist leider verstümmelt, er wäre besonders interessant gewesen. Waren sich die Autoren der Formulierung nicht sicher und wollten sie noch korrigieren?)